一、考试要求
数学科目考试的宗旨是:测试考生的中学、中职数学基础知识、基本技能、基本思想、方法,考查考生的中学、中职数学基本运算能力、逻辑思维能力和运用所学知识分析和解决简单实际问题的能力。
二、考试内容与考核要求
1.集合与充要条件
(1)理解集合的概念及几个特殊的集合;理解元素与集合的关系。
(2)掌握集合的表示法、数集的概念及其相对应的符号。
(3)掌握集合间的关系(子集、真子集、相等)。
(4)理解集合的运算(交集、并集、补集)。
(5)理解充分条件、必要条件、充要条件的概念与判断。
2.不等式
(1)理解不等式的基本性质。
(2)掌握区间的基本概念。
(3)掌握利用二次函数图像解一元二次不等式的方法。
(4)了解含绝对值的一元一次不等式的解法。
(5)求解一元一次不等式和一元一次不等式组。
(6)理解区间、区间的端点、闭区间、开区间、半开区间、有限区间、无限区间的概念。
(7)掌握闭区间、开区间、半开区间、有限区间、无限区间的表示。
(8)会用区间表示不等式解集。
3.函数
(1)理解函数的概念。
(2)理解函数的三种表示法。
(3)会计算函数值和求函数的定义域。
(4)会判断函数的单调性与奇偶性。
(5)了解函数(含分段函数)的简单应用。
4.指数函数与对数函数
(1)理解实数指数幂;理解有理指数幂的概念及其运算法则。
(2)理解幂函数的概念。
(3)理解指数函数的概念、图像与性质。
(4)理解对数的概念(含常用对数、自然对数)。
(5)掌握积、商、幂的对数运算法则。
(6)理解对数函数的概念、图像和性质。
(7)理解指数函数和对数函数的实际应用。
5.三角函数
(1)理解任意角的概念。
(2)理解弧度制概念及其与角度的换算。
(3)理解任意角正弦函数、余弦函数和正切函数的概念。
(4)掌握利用计算器求三角函数值的方法。
(5)理解同角三角函数的基本关系式:sin2α+cos2α=1、tanα=sinα/cosα
(6)理解正弦函数的图像和性质。
(7)理解余弦函数的图像和性质。
(8)理解已知三角函数值求指定范围内的角。
6.数列
(1)理解数列、项、首项、项数、无穷数列、有穷数列、通项或一般项、通项公式的概念。
(2)会求简单数列的通项公式。
(3)理解等差数列、公差、等比数列、公比的概念。
(4)理解公差、公比、通项或一般项、前n项和的字母表示。
(5)掌握等差数列和等比数列的中项公式,通项公式,前n项和公式的运用。
(6)了解等差数列和等比数列的简单实际应用。
7.平面向量
(1)理解数量、向量、向量的模、零向量、单位向量、平行(共线)向量、相等向量、自由向量、负向量、向量的加法、三角形法则、平行四边形法则、和向量、差向量、向量的数乘、向量的线性组合、向量的线性表示、向量的线性运算的概念。
(2)理解向量加法具有的性质和向量数乘运算满足的法则。
(3)理解向量的坐标表示。
(4)掌握向量线性运算、平行(共线)向量的坐标表示。
(5)会计算向量的模。
(6)理解平行(共线)向量的坐标表示。
8.直线和圆的方程
(1)掌握任意两点间的距离公式和线段中点的坐标公式。
(2)理解直线的倾斜角、斜率、横截距、纵截距、斜截式方程、点斜式方程、一般式方程的概念。
(3)理解直线倾斜角的取值范围。
(4)掌握过任意两点的直线的斜率公式。
(5)理解二元一次方程与直线间的关系。
(6)掌握直线的斜截式方程、点斜式方程、一般式方程的确定。
(7)理解两直线平行和垂直的条件及运用。
(8)掌握两相交直线的交点坐标的计算。
(9)掌握点到直线的距离公式。
(10)掌握圆、圆心、半径、圆的标准方程、圆的一般方程的概念。
三、考试形式与试卷结构
1.答题方式:闭卷、笔试.不允许使用计算器.
2. 考试时间:90分钟.
3. 试卷题型:选择题和非选择题.全卷满分150分,试卷结构如下:
题型 | 题量 | 小题分 | 分值 |
单项选择题 | 12 | 5 | 60 |
填空题 | 6 | 5 | 30 |
解答题 | 3 | 20 | 60 |
合计 | 21 | —— | 150 |
2025年咸宁市“一村多名大学生计划”单独招生考试
《数 学》科目样卷示例
(本试卷共21题,满分150分)
一、单项选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个备选项中,只有一项是符合题目要求的,请将其选出。未选、错选或多选均不得分)
1. 已知集合A={1,2,3},集合B={2,3,4,5,6,7},则A⋂B( )。
A.{2,3} B.{1,2,3} C.{1,2,3,4,5,6,7} D.Ø
2.下列运算正确的是( )
A.a³+a5=a8; B. a3⋅a5=a8 C.(a3)5=a8 D.a15÷a5=a³
二、填空题(本题共6小题,每小题5分,共30分,将正确答案填在题中的横线上)
13. 如果直线l经过点(2,0)和点(5,3),那么直线l的斜率是 。
14. 等差数列中,a1 =1,a3=7,,则公差d= 。
三、解答题(本大题共3小题,每小题20分,共60分,应写出文字说明,证明过程或演算步骤)
19.X取什么范围内的实数时,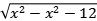 有意义。
有意义。
