一、考试要求
数学科目考试的宗旨是:测试考生的中学、中职数学基础知识、基本技能、基本思想和方法,考查考生的中学、中职数学基本运算能力、逻辑思维能力和运用所学知识分析和解决简单实际问题的能力。考试要求按照知识要求从低到高分为如下三个层次:
1.了解:初步知道知识的含义及其简单应用。
2.理解:懂得知识的概念和规律(定义、定理、法则等),以及与其他相关知识的联系。
3.掌握:能够应用知识的概念和规律去解决一些问题。
二、考试内容与考核要求
1.集合与充要条件
(1)理解集合,元素,数集,空集,有限集,无限集,子集,真子集,集合相等,交集,并集,全集,补集的概念,并进行相关运算。
(2)理解集合中元素确定性、互异性、无序性的特性。
(3)理解元素与集合的字母表示及关系符号。
(4)掌握常用数集、空集、全集的字母表示。
(5)掌握集合的列举与描述表示法。
(6)了解平面内点集的表示法。
(7)掌握集合子集、真子集、集合相等的关系符号。
(8)掌握交集、并集、补集的表示法。
(9)掌握交集、并集、补集的运算及性质。
(10)理解充分条件、必要条件、充要条件的概念。
(11)掌握充分条件、必要条件、充要条件的判断。
2.不等式
(1)掌握比较实数大小的方法。
(2)掌握不等式加法、乘法、传递的基本性质。
(3)理解区间、区间的端点、开区间、闭区间、半开区间、有限区间、无限区间的概念。
(4)掌握开区间、闭区间、半开区间、有限区间、无限区间的表示。
(5)掌握一元一次不等式、一元二次不等式的求解及应用。
(6)掌握含绝对值不等式的解法。
(7)掌握不等式解集的区间表示。
3.函数
(1)理解函数、自变量、定义域、值域、解析法、列表法、图像法、单调性、增函数、减函数、单调区间、增区间、减区间、奇偶性、奇函数、偶函数、非奇非偶函数、分段函数的概念。
(2)掌握函数定义域、值域的求解。
(3)了解函数概念中两个要素的应用。
(4)了解函数解析法与列表法的应用。
(5)了解平面内任意点的对称点的坐标特征。
(6)掌握函数单调性与奇偶性的判断。
(7)了解分段函数的建立。
(8)了解函数的简单实际应用。
4.指数函数与对数函数
(1)掌握实数指数幂的运算法则。
(2)理解幂函数、指数函数、对数、对数的底、真数、常用对数、自然对数、对数函数的概念。
(3)了解指数函数的图像与性质及应用。
(4)了解指数式与对数式互化的条件。
(5)掌握对数的基本性质。
(6)了解常用对数与自然对数的记法。
(7)掌握积、商、幂的对数运算法则。
(8)掌握对数函数的图像与性质及应用。
5.三角函数
(1)理解角、正角、负角、零角、任意角、象限角、界限角、终边相同的角、弧度角、角度制、弧度制的概念。
(2)掌握象限角、界限角、终边相同的角的集合表示。
(3)掌握角度与弧度的互化关系。
(4)了解圆弧长、半径、弧度角的关系及应用。
(5)理解任意角的正弦函数、余弦函数、正切函数的概念。
(6)了解各象限角的正弦函数值、余弦函数值、正切函数值的正负号判断。
(7)熟记界限角的正弦函数值、余弦函数值、正切函数值。
(8)掌握同角正弦函数、余弦函数、正切函数的基本关系式。
(9)掌握含有正弦函数、余弦函数、正切函数的式子的化简与求值。
(10)掌握任意角的正弦函数、余弦函数、正切函数的诱导公式的运用。
(11)了解正弦函数、余弦函数的图像和性质。
(12)掌握已知正弦函数值、余弦函数值、正切函数值求指定范围内的特殊角的方法。
6.数列
(1)理解数列、项、首项、项数、有穷数列、无穷数列、通项或一般项、通项公式的概念。
(2)会求简单数列的通项公式。
(3)理解等差数列、公差、等比数列、公比的概念。
(4)理解公差、公比、通项或一般项、前n项和的字母表示。
(5)掌握等差数列和等比数列的中项公式,通项公式,前n项和公式的运用。
(6)了解等差数列和等比数列的简单实际应用。
7.平面向量
(1)了解数量、向量、向量的模、零向量、单位向量、平行(共线)向量、相等向量、自由向量、负向量、向量的加法、三角形法则、平行四边形法则、和向量、差向量、向量的数乘、向量的线性组合、向量的线性表示、向量的线性运算的概念。
(2)了解向量加法具有的性质和向量数乘运算满足的法则。
(3)了解向量的坐标表示。
(4)掌握向量线性运算、平行(共线)向量的坐标表示。
(5)理解两向量夹角、内积的概念。
(6)了解两向量夹角的取值范围。
(7)了解向量内积的几个重要结果和满足的运算律。
(8)掌握向量内积的坐标表示。
(9)掌握向量的模的计算。
(10)了解平行(共线)向量和垂直向量的坐标表示。
8.直线和圆的方程
(1)掌握任意两点间的距离公式和线段中点的坐标公式。
(2)理解直线的倾斜角、斜率、横截距、纵截距、点斜式方程、斜截式方程、一般式方程的概念。
(3)了解直线倾斜角的取值范围。
(4)掌握过任意两点的直线的斜率公式。
(5)理解二元一次方程与直线间的关系。
(6)掌握直线的点斜式方程、斜截式方程、一般式方程的确定。
(7)了解两直线平行和垂直的条件及运用。
(8)掌握两相交直线的交点坐标的计算。
(9)了解两直线夹角的概念及取值范围。
(10)掌握点到直线的距离公式。
(11)理解圆、圆心、半径、圆的标准方程、圆的一般方程的概念。
(12)了解确定圆的条件。
(13)掌握圆的标准方程、一般方程的确定。
(14)了解直线和圆的位置关系的判断。
(15)了解直线和圆的方程的简单实际应用。
三、考试形式与试卷结构
1.答题方式:闭卷、笔试.不允许使用计算器.
2. 考试时间:90分钟.
3. 试卷题型:选择题和非选择题.全卷满分150分,试卷结构如下:
题型 | 题量 | 小题分 | 分值 |
单项选择题 | 12 | 5 | 60 |
填空题 | 6 | 5 | 30 |
解答题 | 3 | 20 | 60 |
合计 | 21 | —— | 150 |
2024年咸宁市“一村多名大学生”计划单独招生考试
《数 学》科目样卷示例
(本试卷共21题,满分150分)
一、单项选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个备选项中,只有一项是符合题目要求的,请将其选出。未选、错选或多选均不得分)

二、填空题(本题共6小题,每小题5分,共30分,将正确答案填在题中的横线上)
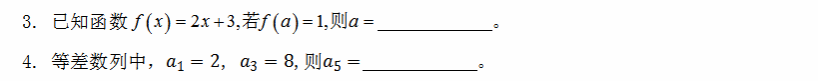
三、解答题(本大题共3小题,每小题20分,共60分,应写出文字说明,证明过程或演算步骤)

